Sliding window maximum

Link: https://leetcode.com/problems/sliding-window-maximum/

Solution:

Topics: stack, deque, sliding window

Intuition
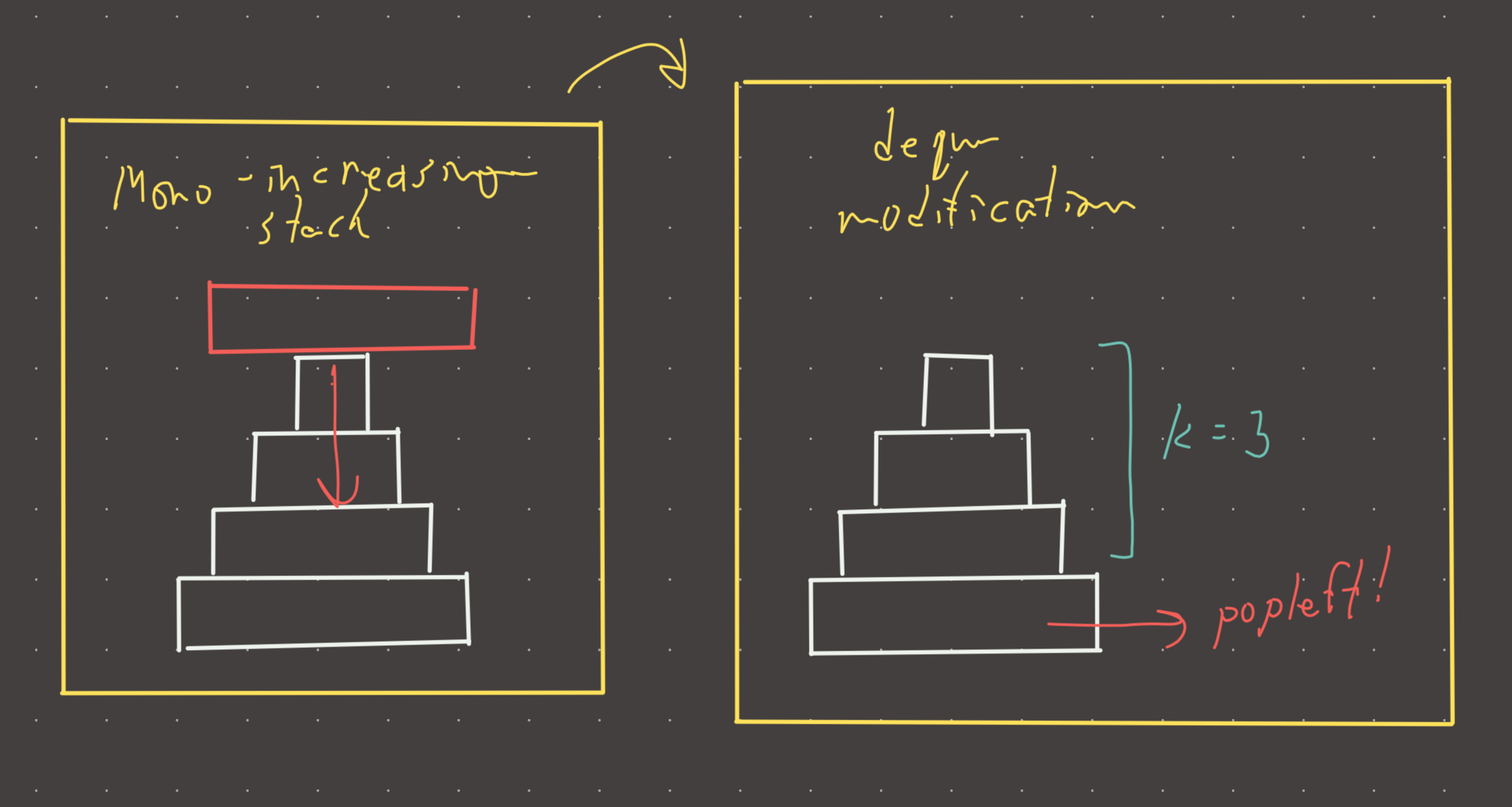
Kind of tricky problem, my first intuition was to use a heap which actually works very well but the efficiency is a little bit worse than optimal (although still good). The most optimal solution is pretty clever. We use a monotonically increasing stack and just pop off the left side to keep all the values in the window.

Overall, its not that hard to come up with, but the optimal solution was not the first thing that came to my mind.

Implementation

def win_max(nums, k):
	stack = deque()
	res = []
	for i in range(len(nums)):
		while stack and stack[-1][0] <= nums[i]:
			stack.pop()
		stack.append((nums[i], i))
		if stack[0][1] < i-k+1:
			stack.popleft()
		if i >= k-1:
			res.append(stack[0][0])
	return res
#time: o(n)
#memory: o(k)

Visual

Review 1
Fun problem! I thought initially that there should be a result for every index so I wrote some dumb and unnecessary code. Basically, you can start appending results on the first complete sliding window:

k = 3
nums = [-7,-8,7,5,7,1,6,0]
              ^
              start adding to result here.

Review 2
Not the greatest implementation above. It’s better to simply push indices to the stack and clean out the front of the stack if it’s outside the window. The key insight for these type of problems (max/min in window) is that we don’t need to consider smaller numbers (in the case of max) after bigger ones have already been seen…hence we can pop them off the stack to maintain decreasing order (in the case of max).

Implementation

 
def max_win(nums, k):
	res = []
	dec_stack = deque()
	l = 0
	for r in range(len(nums)):
		while dec_stack and dec_stack[0] < l: #remove from window
			dec_stack.popleft()
 
		while dec_stack and nums[dec_stack[-1]] < nums[r]: #maintain decreasing property
			dec_stack.pop()
		dec_stack.append(r)
 
		if r - l + 1 == k: #add to result and shrink window
			res.append(nums[dec_stack[0]])
			l += 1
	return res

Tagging this as hard because the linear solution is tricky.

review
hard