Course schedule II

Link: https://leetcode.com/problems/course-schedule-ii/

Solution:

DSA: graph, topological order, DFS

Intuition
This problem is a classic topological ordering. Its made slightly more complicated by the fact that not all of the courses my be in the list of prerequisites. A course with no prerequisites can automatically be taken, but there is no need for special handling.

Just make sure to add every course to the adjacency list, because there is no guarantee that it will be inside the prerequisites list. And make sure to include cycle detection, if there is a cycle, return and empty array.

For example:

num_courses = 5
prerequsites = []
 
result = [0, 1, 2, 3, 4] #or any ordering for that matter because if there are no prerequisites, then any course can be taken at any time. Hence why the promblem statement asked for ANY ordering, because there are many. 

Implementation

def topo_order(num_courses, prerequisites):
	adj = {i:[] for i in range(num_courses)}
	for course, prereq in prerequisites:
		adj[course].append(prereq)
 
	res = []
	def dfs(node, visited, visiting):
		if node in visiting:
			return False
		if node in visited:
			return True
 
		visiting.add(node)
		for neighbor in adj[node]:
			if not dfs(neighbor, visited, visiting):
				return False
		visiting.remove(node)
		visited.add(node)
		res.append(node)
 
	visited = set()
	visiting = set()
	for course in range(num_courses):
		if not dfs(course, visited, visiting):
			return []
	return res
 
#NOTE: the reason why it does not matter which course we start from is because no matter where we start, all of its children get added to to res. For example, if we randomly manage to start at the last possible course, then all prerequisite courses would get added in one single traversal. If not, then the nodes and children that we do see again, go into visited and we have a base-case that prohbits appending previously seen nodes to the result. 

Visual

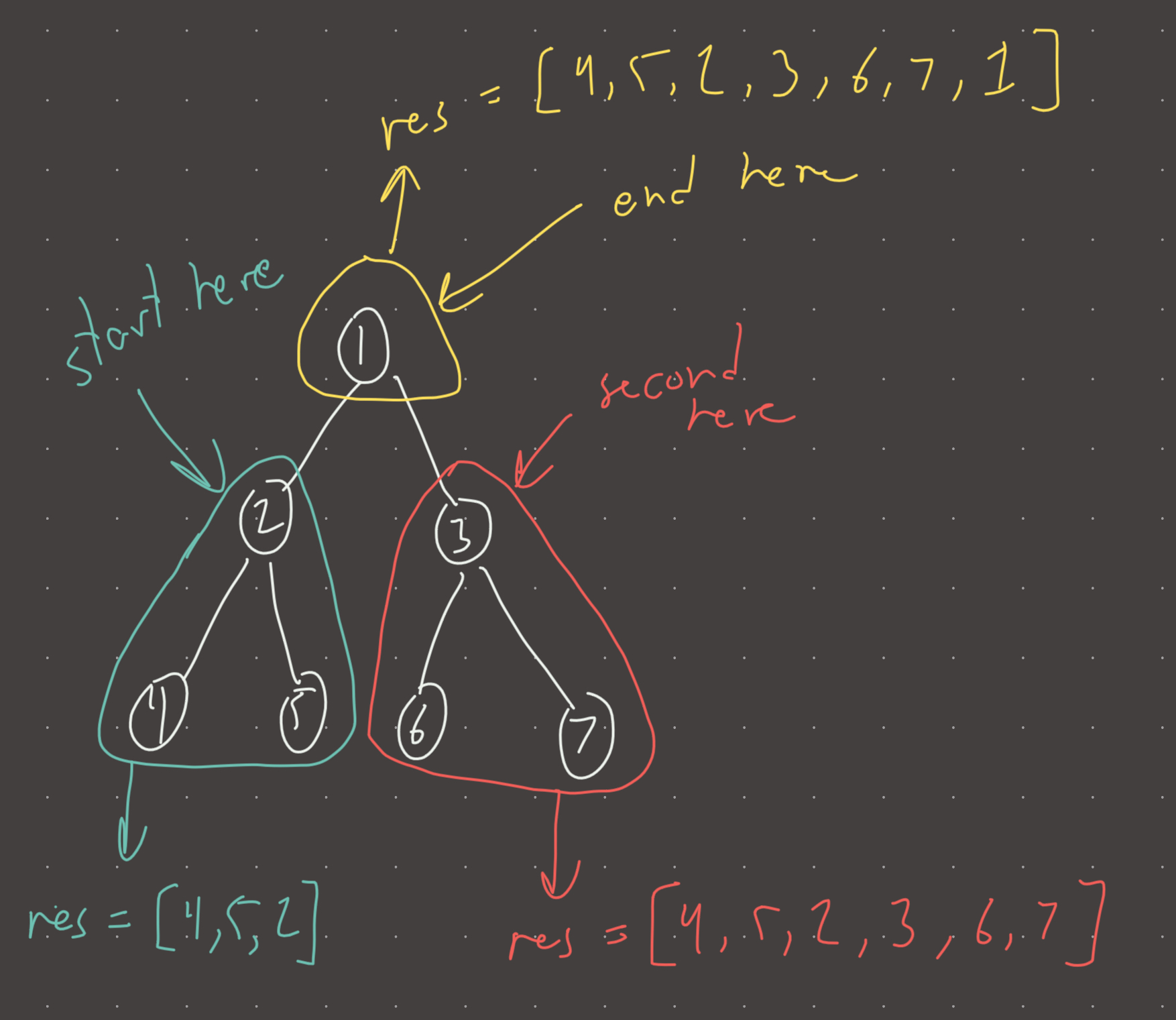
Review 1
I again spent too much time thinking about where to start from…for topological ordering it does not matter at all because we append to the topologically ordered list. Appending a node to a list after all it’s children have been visited guarantees that all dependencies are added to the list before the node itself! If that node is itself a dependency of another node, it’s parents will be added later on to the list; thus the topological ordering is maintained.

One more thing about this problem. It’s important to frame the relationships correctly. The last course to take (the one with the most prerequisites) is the root of the graph, and the courses that have no dependencies are the leaves. If we set up the problem this way, then the course with the most dependencies is the last one added to list…which is the ordering that is demanded in the problem statement! If we set up the problem in the opposite way, then the resulting topological array will be in reverse order…not a terrible outcome but we will have to do a spurious reversal.

review