Link: https://leetcode.com/problems/longest-arithmetic-subsequence-of-given-difference/
Solution:
Topics: hash map
Intuition
Cool problem. It took me for a bit of a loop at first because immediately when I see “subsequence” I think of DP…and indeed we can solve this with DP but it results in memory limit exceeded because the DP approach requires caching a function with 3 (possibly 2) parameters…so we get n**3 memory complexity or n**2 in the best case.
Upon further analysis though, there is enough to work with here for a purely greedy solution with the help of a hash map. We are given difference which the arithmetic subsequence must obey…so we can use difference to compute the would-be previous value in a potential subsequence (classic has/needs pattern). If this would-be element has been seen before, we set the current value to has[num] = has[prev] + 1.
There are some parallels here to the reservoir pattern in the sense that the hash-map is our reservoir in this case…but this reservoir is not cumulative in the same way that counting new subarrays is (because n new subarrays are created for every element added).
Implementation
def longest_diff(arr, difference):
res = 0
has = {}
for num in arr:
prev = num - difference
if prev in has:
has[num] = has[prev] + 1
else:
has[num] = 1
res = max(res, has[num])
return res
#time: o(n)
#memory: o(n)Mnemonic
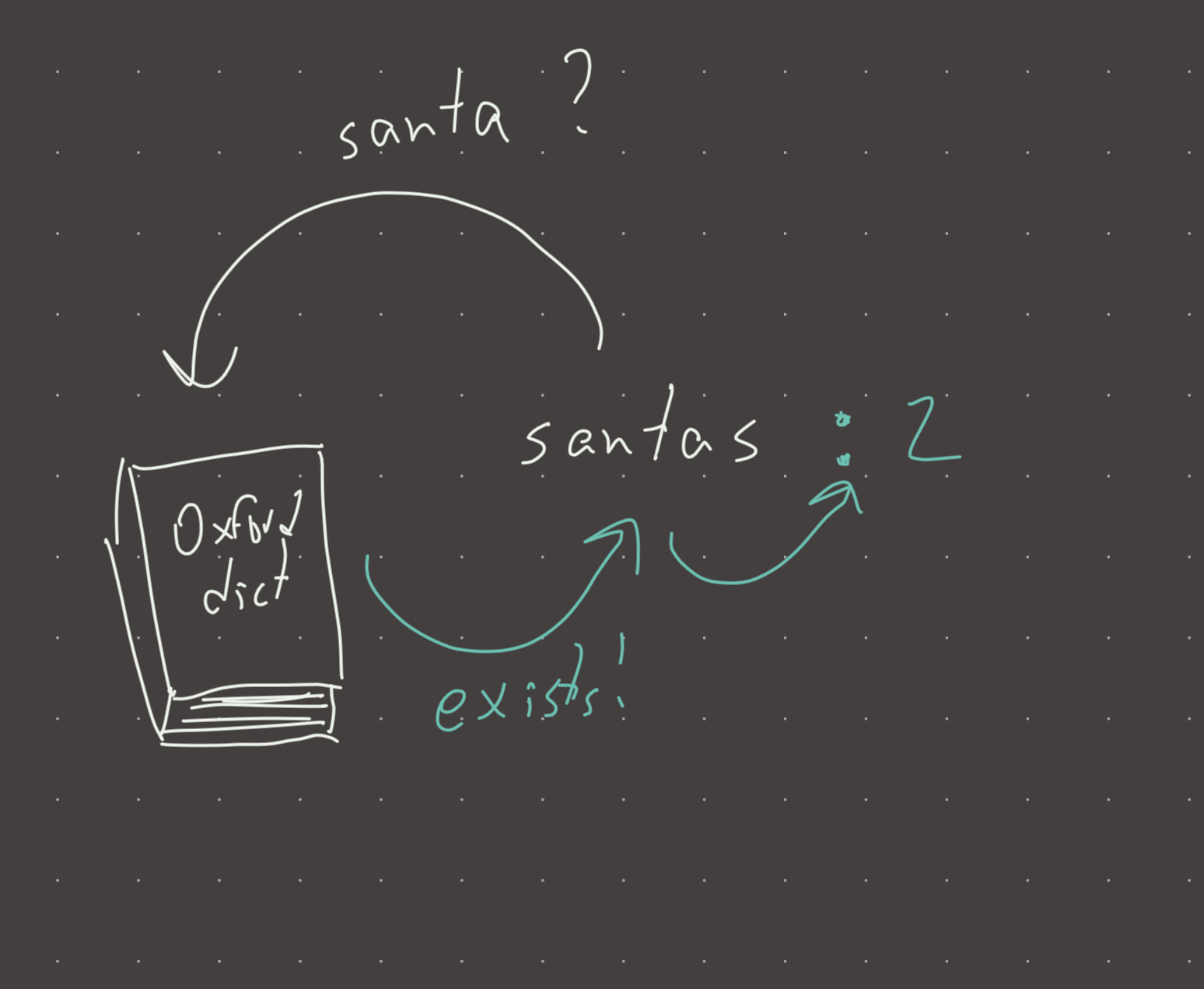
You are looking for the longest word made up of another word minus the last letter. For example ever -> every. You reach the word santas, remove the last letter to get santa. Check your dictionary to see if santa is a valid word. It is a valid word. Make a note beside the dictionary entry for santas that it represents 2 words. If the word santast was a word (it is not), Its value would by 3 because we would go back to the entry for santas and increment it by 1 for santast.
Visual
Review 1
Amazingly, I did not fall into the DP trap! I guess this is a sign of improvement, so ill take it (even for a question as easy as this one).