Link: https://leetcode.com/problems/binary-tree-maximum-path-sum/
Solution:
Topics: DFS, Diameter of a binary tree, Path sum II
Intuition
This is a great little path finding problem. Basically it’s a path sum problem with one catch: the path doesn’t have to be root-to-leaf…it can be any connected path within the tree. This is more interesting because the node values can be negative so we can’t necessarily take every node value.
The key insight comes down to making a decision at every node. At every node we must consider if the node itself is the max path, if the node plus the left is the max path, if the node plus the right is the max path, and if the node plus the right and left is the max path. We determine the max combination and then we propagate that result up the tree to enable the same decision making in the parent nodes.
A key consideration is the fact that if the max path at a node is node.val+left+right, we cannot propagate that up the tree because it would create a path with a node that has two adjacent connections, so for propagation we must choose between node.val, node.val+left, node.val+right. However, we still have to consider node.val+left+right as the max path even though we cannot propagate it.
The logic is not too different from Diameter of a binary tree, but we are propagating sums rather than number of nodes.
Implementation
def max_path_sum(root):
self.res = float('-inf')
def dfs(node):
if node is None:
return 0
left = dfs(node.left)
right = dfs(node.right)
max_path = max(node.val, node.val+left, node.val+right)
self.res = max(self.res, max_path, node.val+left+right)
return max_path
dfs(root)
return self.res
#time: o(n)
#memory: o(n)Visual
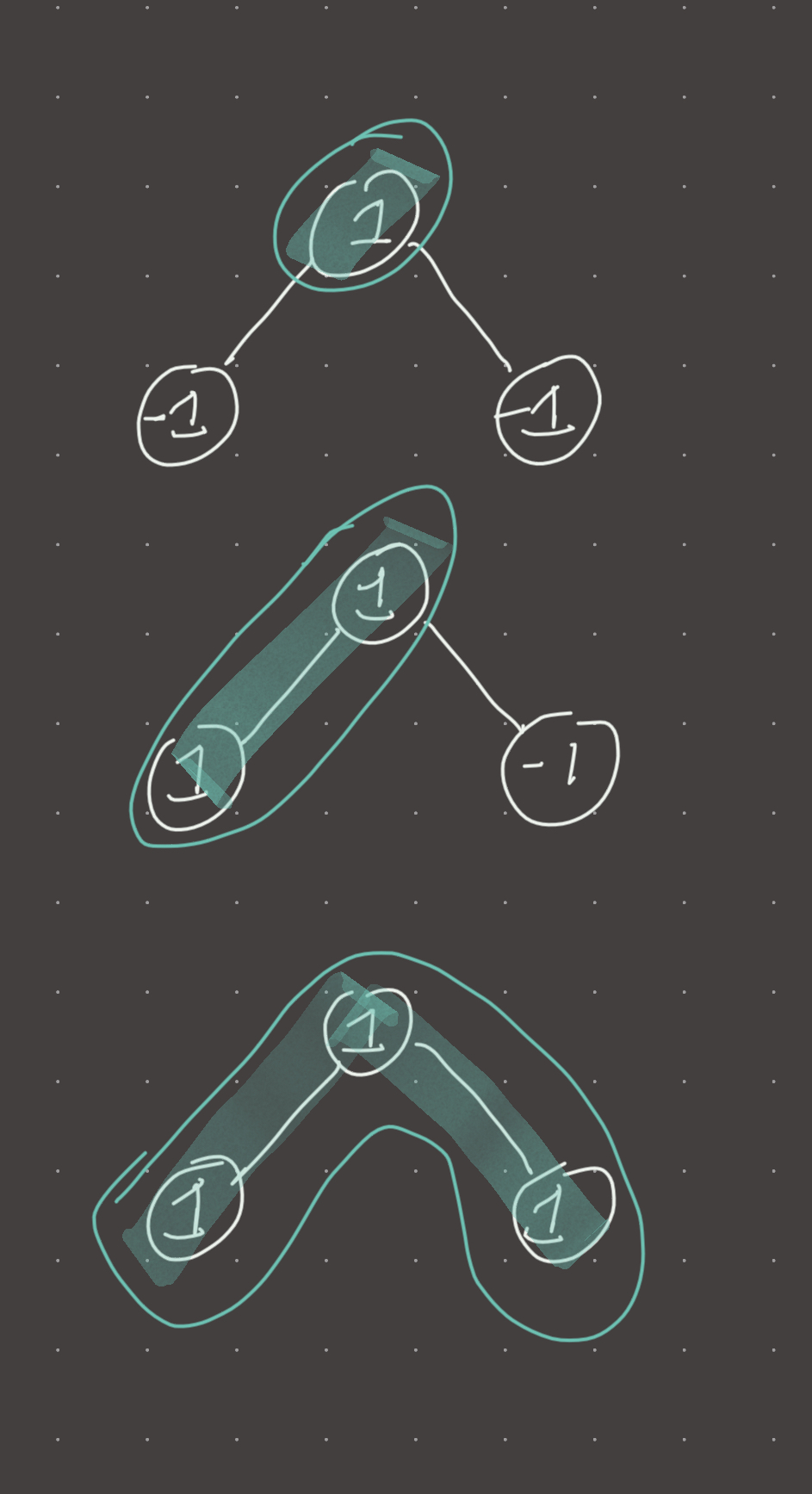
Review 1
Found the solution fast. Spent a bit of time trying to figure out if the path had to terminate at a leaf (it does not). Don’t forget that any connected path is a possible max path (including a single node).