Path sum II

Link: https://leetcode.com/problems/path-sum-ii/

Solution:

Topics: DFS, back tracking

Intuition
This is a simple DFS problem but with a notable edge case. The base-case must be triggered at the leaf node, not on a null pointer…why? Because terminating at null would result in valid paths being added twice: once for left null pointer and once for right null pointer!

Implementation (DFS)

def path_sum2(root, targetSum):
	res = []
	def dfs(node, path, total):
		if node is None:
			return
		total += node.val
		path = list(path) + [node.val]
		if node.left is None and node.right is None and total == targetSum:
			res.append(path)
			return 
		dfs(node.left, path, total)
		dfs(node.right, path, total)
	dfs(root, [], 0)
	return res
		
#time:
#memory:

There is also a great backtracking solution for further optimization. Basically in the above solution we are propagating a new copy of the path at every node. This is very inefficient from a memory complexity standpoint…and also time because a copying a list is an o(n) operation.

We can use back-tracking to optimize this recursion and keep the current path and total in global variables. This is possible because of the nature of DFS traversals…when we reach a leaf, the path gets popped off until an unexplored path is reached:

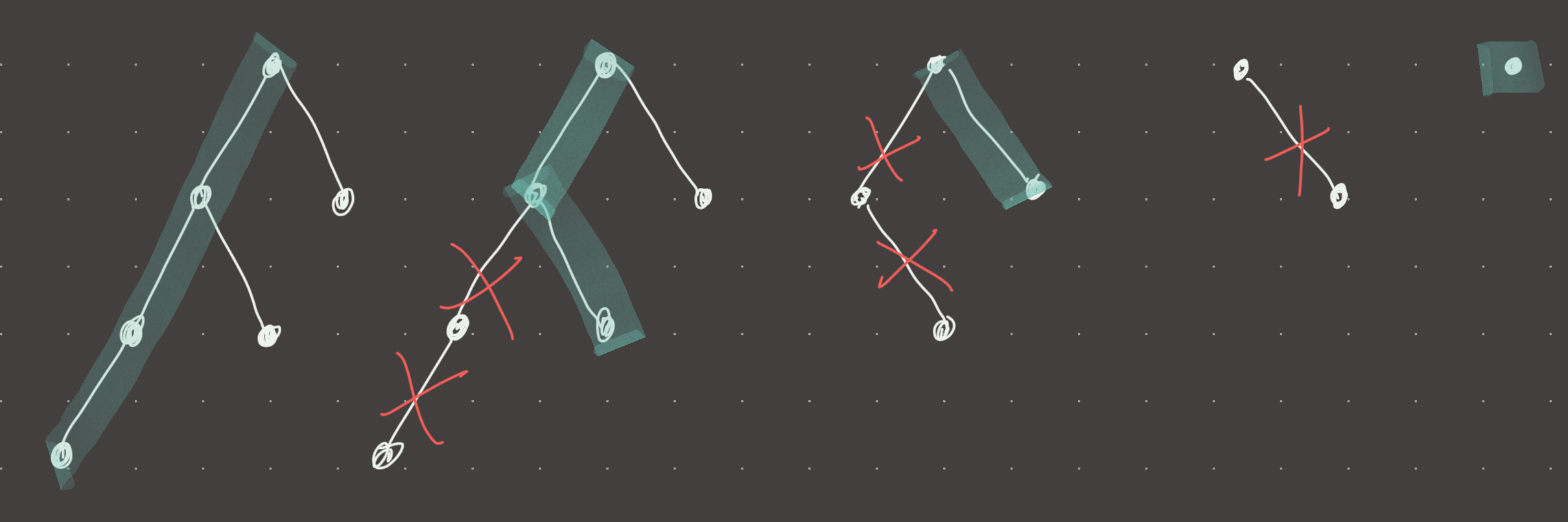
Essentially the DFS traversal “climbs back” up the path it came before exploring the new leftmost path. Backtracking leverages this property to save resources.

Implementation (Backtracking)

def path_sum2(root, targetSum):
	res = []
	path = []
	self.path_sum = 0
	def dfs(node):
		if node is None:
			return 
			
		path.append(node.val)
		self.path_sum += node.val
		if (node.left is None and node.right is None
			and self.path_sum == targetSum):
				res.append(list(path))
		dfs(node.left)
		dfs(node.right)
		self.path_sum -= path.pop()
 
	dfs(root)
	return res
	

Review 1
Really like the backtracking approach. I think I had a breakthrough when I originally did this problem, because i’m using this approach everywhere I can now. It’s just so much better than propagating the state.

review