Link: https://leetcode.com/problems/minimum-cost-to-convert-string-ii
Solution:
Topics: Dijkstra’s, DP
Intuition
This is a very challenging problem, and I honestly could not come up with a way to approach it. Fortunately, after reading some solutions I found an approach that makes sense to me.
Transformations will be referred to as the tuple (original, changed, cost)
Lets think about this problem on a high level. Clearly this will involve a search and we will be branching out with all the legal transformations for that position. So what is a legal transformation in this context? A legal transformation will be one that can convert a substring starting at a particular index into the target substring of that same range.
Lets look at a base-case:
trans = [('a', 'b', 1)]
source = a
target = b
We can see ('a', 'b', 1) is a legal transformation here because it will have converted the source into the target at cost 1.
Of course there is more to this problem, because we could potentially need many transformations to turn source into target.
For example:
trans = [('a', 'b', 1), ('b', 'a', 1)]
source = ab
target = ba
In this case, we will have to use both transformations in order to convert source into target at a total cost of 2.
However, we can imagine that there are multiple ways to convert source into target, and we are interested in the one with the lowest cost!
For example:
trans = [('a', 'b', 1), ('b', 'a', 1), (ab, ba, 1)]
source = ab
target = ba
In this case, we can see that using the third transformation is the most optimal.
So the idea here is to look at each substring from i to len(source), and determine the lowest cost of converting source[i:j] into target[i:j] if such a transformation exists! Or in other words, we are looking for the cheapest path between source[i:j] and target[i:j]. If such a path exists, we can branch off and shift i to j+1 because everything up until i would be considered transformed.
We can use either Dijkstra’s or optimized BFS to find the shortest path in a weighted graph! But first lets understand how exactly we can build this graph. We would generally use an adjacency list, but there is one important caveat. There could me many legal transformations that are useless to us. Why?
Because of this:
trans = [('a', 'b', 1), ('a', 'b', 2)]
If we look at the two transformations here, we can see that the second one is useless to us because its the same transformation as the first, but with a higher cost, so it should be discarded.
So essentially, as we build our adjacency list, we must keep the minimum cost for duplicate transformations if the transformation already exists in the list! What this means is that using a list to store neighbouring nodes is very inconvenient because we potentially need to update transformations with smaller costs, and we want to do this in o(1) time.
For example:
trans = [('a', 'b', 2), ('a', 'c', 1), ('a', 'c', 1)]
i = 0
adj = {
'a': [('b', 2)]
}
i = 1
adj = {
'a': [('b', 2), ('c', 1)]
}
i = 2
adj = {
'a': [('b', 2), ('c', 1)]
^ we must iterate through the whole list (potentially)
to find 'b' and update its new cost to 1.
}
The logical solution to avoid o(n) lookups is to store neighbours in a hash map, that way we can lookup neighbours in o(1) time and update costs. We can convert these neighbours back to a list of tuples, but it will not make much difference. So we get to our first block of code:
Building the list:
adj = {}
for parent, neighbor, price in zip(original, changed, cost):
if parent not in adj:
adj[parent] = {} #init the hash map
if neighbor in adj[parent]: #found duplicate transformation
adj[parent][neighbor] = min(adj[parent][neighbor], price) #take the min
else:
adj[parent][neighbor] = priceNow, we have a graph that can be used to run a Dijkstra’s between two nodes, so lets write a function that returns the minimum cost between two strings, or infinity if no such connection is possible.
Dijkstra:
def min_cost(start, end):
queue = [(0, start)] #init the heap with cost = 0 and start string.
costs = {start: 0} #init the costs with the same
while queue:
cost, curr = heappop(queue)
if curr == end:
return cost
if curr not in adj:
continue #no transformations
for neighbor, price in adj[curr].items(): #iterate through neigbors
new_cost = cost + price
if neighbor not in costs:
costs[neighbor] = float('inf')
if new_cost < costs[neighbor]:
costs[neighbor] = new_cost
heappush(queue, (new_cost, neighbor))
return float('inf') Now we can build our recursive DP function and use our Dijkstra function to verify (and get min cost of) valid transformations:
@cache
def dfs(i):
if i >= len(source):
return 0
cost = float('inf') if source[i] != target[i] else dfs(i+1)
for j in range(i+1, len(source)+1):
sub_source = source[i:j]
sub_target = target[i:j]
min_c = min_cost(sub_source, sub_target)
if min_c != float('inf'):
cost = min(cost, min_c + dfs(j))
return costIn the above, we are checking every substring to find a valid transformation, but we can optimize this greatly with a trie! The key is to find all valid transformations in that range, and we can do it much faster by converting all transformations into trie! As it happens, we are already iterating through all the transformations when we build our graph, so we can modify that code to build our trie.
trie = {}
adj = {}
for parent, neighbor, price in zip(original, changed, cost):
if parent not in adj:
adj[parent] = {} #init the hash map
if neighbor in adj[parent]: #found duplicate transformation
adj[parent][neighbor] = min(adj[parent][neighbor], price) #take the min
else:
adj[parent][neighbor] = price
curr = trie
for char in parent:
if char not in curr:
curr[char] = {}
curr = curr[char]
curr['*'] = parentAnd now lets implement trie logic into the DP function:
@cache
def dfs(i):
if i >= len(source):
return 0
cost = float('inf') if source[i] != target[i] else dfs(i+1)
curr_trie = trie
sub_target = ''
for j in range(i, len(source)):
char = source[j]
sub_target += target[j]
if char not in curr_trie:
break
if '*' in curr_trie[char]:
sub_source = curr_trie[char]['*']
min_c = min_cost(sub_source, sub_target)
if min_c != float('inf'):
cost = min(cost, min_c + dfs(i+len(sub_source)))
curr_trie = curr_trie[char]
return costNow putting it all together…
Implementation
trie = {}
adj = {}
for parent, neighbor, price in zip(original, changed, cost):
if parent not in adj:
adj[parent] = {} #init the hash map
if neighbor in adj[parent]: #found duplicate transformation
adj[parent][neighbor] = min(adj[parent][neighbor], price) #take the min
else:
adj[parent][neighbor] = price
curr = trie
for char in parent:
if char not in curr:
curr[char] = {}
curr = curr[char]
curr['*'] = parent
def min_cost(start, end):
queue = [(0, start)] #init the heap with cost = 0 and start string.
costs = {start: 0} #init the costs with the same
while queue:
cost, curr = heappop(queue)
if curr == end:
return cost
if curr not in adj:
continue #no transformations
for neighbor, price in adj[curr].items(): #iterate through neigbors
new_cost = cost + price
if neighbor not in costs:
costs[neighbor] = float('inf')
if new_cost < costs[neighbor]:
costs[neighbor] = new_cost
heappush(queue, (new_cost, neighbor))
return float('inf')
@cache
def dfs(i):
if i >= len(source):
return 0
cost = float('inf') if source[i] != target[i] else dfs(i+1)
curr_trie = trie
sub_target = ''
for j in range(i, len(source)):
char = source[j]
sub_target += target[j]
if char not in curr_trie:
break
if '*' in curr_trie[char]:
sub_source = curr_trie[char]['*']
min_c = min_cost(sub_source, sub_target)
if min_c != float('inf'):
cost = min(cost, min_c + dfs(i+len(sub_source)))
curr_trie = curr_trie[char]
return cost
res = dfs(0)
return res if res != float('inf') else -1
#time: o(n*m*(mlogm)) n=len(source) m = len(transformations)
#memory: max(o(n), o(m))Mnemonic
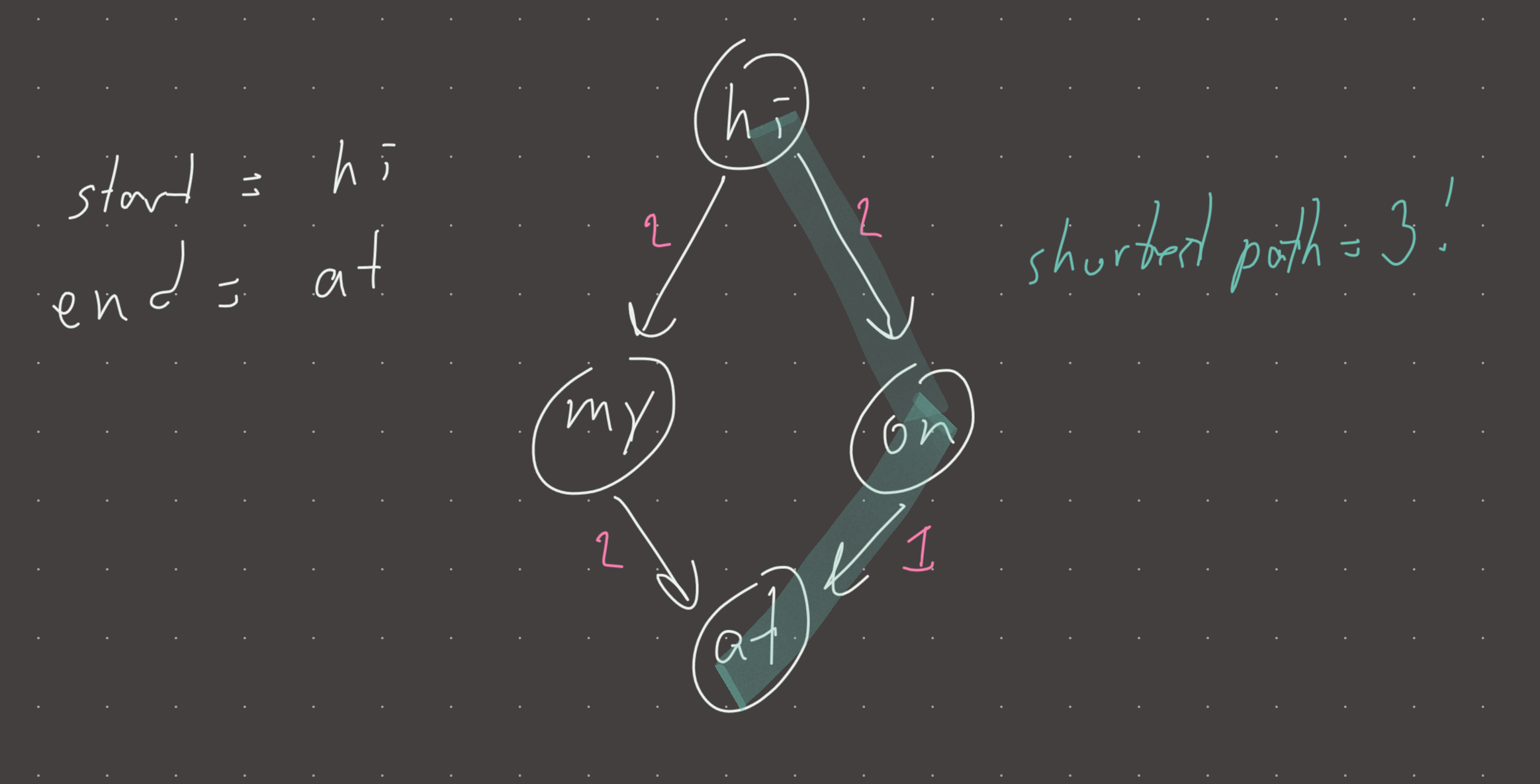
Think one string at a time. You gave a graph of strings and we want the shortest path in the weighted graph between start_string and end_string! ([Dijkstra’s])
Visual
Review 1
Truly an awesome problem! I found the right approach and every optimization fairly quickly but I missed trie search to optimize the DP! Very pleased with my progress on this problem. This problem is pretty close to Word break II.
Review 2
Again found the right approach pretty fast (DP+dijkstra) but missed the trie optimization.