Link: https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/
Solution:
Topics: DFS, bitwise, Reordered power of 2
Intuition
The traversal part of this problem should be fairly obvious. A DFS traversal will take us through all root-to-leaf paths. Of course we need to save information about each path to evaluate if it is pseudo palindromic or not, but what is the least amount of information we can store?
One way is to store every value in the path is a string, and then evaluate if its pseudo palindromic at the leaf node. A pseudo-palindromic frequency map will have at most one odd count.
path = '11112'
freq = {
1: 4,
2: 1,
}
#there is only one odd count, so a palindrome can be made: 11211
The issue with this approach is that storing the entire path will consume lots of memory, and since the problem indicates that node values can only be in the range 1-9, we can keep a list of length 9 to continuously update the frequency of the path.
path = '1111111111111111222'
freq = [0,0,0,0,0,0,0,3,16]
#the memory compression is significant
But we can do even better than that. Why must we store the entire count when all that is relevant to the problem is if the count is even or odd? We can just increment by one if the current count is zero or decrement by one if the current count is 1! In this way, we can store even less information.
path = '1111111111111111222'
freq = [0,0,0,0,0,0,0,1,0]
#even more memory efficient
But its possible to do even better than this! At this point we are only storing binary information in the list, so its possible to just keep all of this information in a bit and use bitwise operations to determine if the path is pseudo-palindromic! How?
Toggle the bit:
bit = 0 # bitwise = 000000000
#lets say the first node value in our path is 1, how do we store that in our bit
#an integer bit is dynamic in python, but in most languages an integer consumes 32 bits of memory...in our case it is an integer we are concerned with because we set our bit to 0. For our purposes, the only part of the bit that is relevant is the first 9 (one for each possbile digit).
node.val = 1
#we want our bit to now look like this: 000000001, how?
#create a bitmask 000000001 and XOR with our bit. The XOR operator flips our bit in every position where our mask is 1.
mask = (1 << node.val-1)
# above line will create 000000001 for node.val = 1, and 100000000 for node.val = 9
bit = bit ^ mask
#this line will toggle the bit in the position of the 1 in the mask. In our case, toggling is all we require because we only need to know in the frequency is even or odd. Toggle twice = even, Toggle 3 times = odd.Check if at most 1 bit is flipped:
#if (at most) one bit is flipped, the path is pseudo-palindromic
#how do we check that with bitwise operations?
#The same way we check power of 2!
if bit & (-bit) == bit:
number_of_pseudo_palindromes += 1
#how does this work?
#A power of 2 has a unique property in binary...there is only one bit flipped.
# 1 = 00001
# 2 = 00010
# 4 = 00100
# 8 = 01000
# 16 = 10000
-bit
#this makes the integer negative, but what does this do to the bit?
#it sets every bit to the reverse except the rightmost bit, so 000000001 would become 111111111.
bit & (-bit)
#the & operator sets every bit to 0 unless both bits are 1! so 000000001 & 111111111 would be 000000001.
if bit & (-bit) == bit:
# we can see above that for this example, 000000001 & 111111111 does indeed equal the original bit, which indicates that this is fact a power of 2, ergo, also representing a path that is pseudo-palidromic
Implementation
def pseudo_palin_count(root):
res = 0
def dfs(node, bit):
if node is None:
return
bit = bit ^ (1 << node.val - 1) # -1 to keep the bit as short as possible
if node.left is None and node.right is None:
if bit & (-bit) == bit:
nonlocal res
res += 1
dfs(node.left, bit)
dfs(node.right, bit)
dfs(root, 0)
return res
#time: o(n)
#memory: o(n)Visual
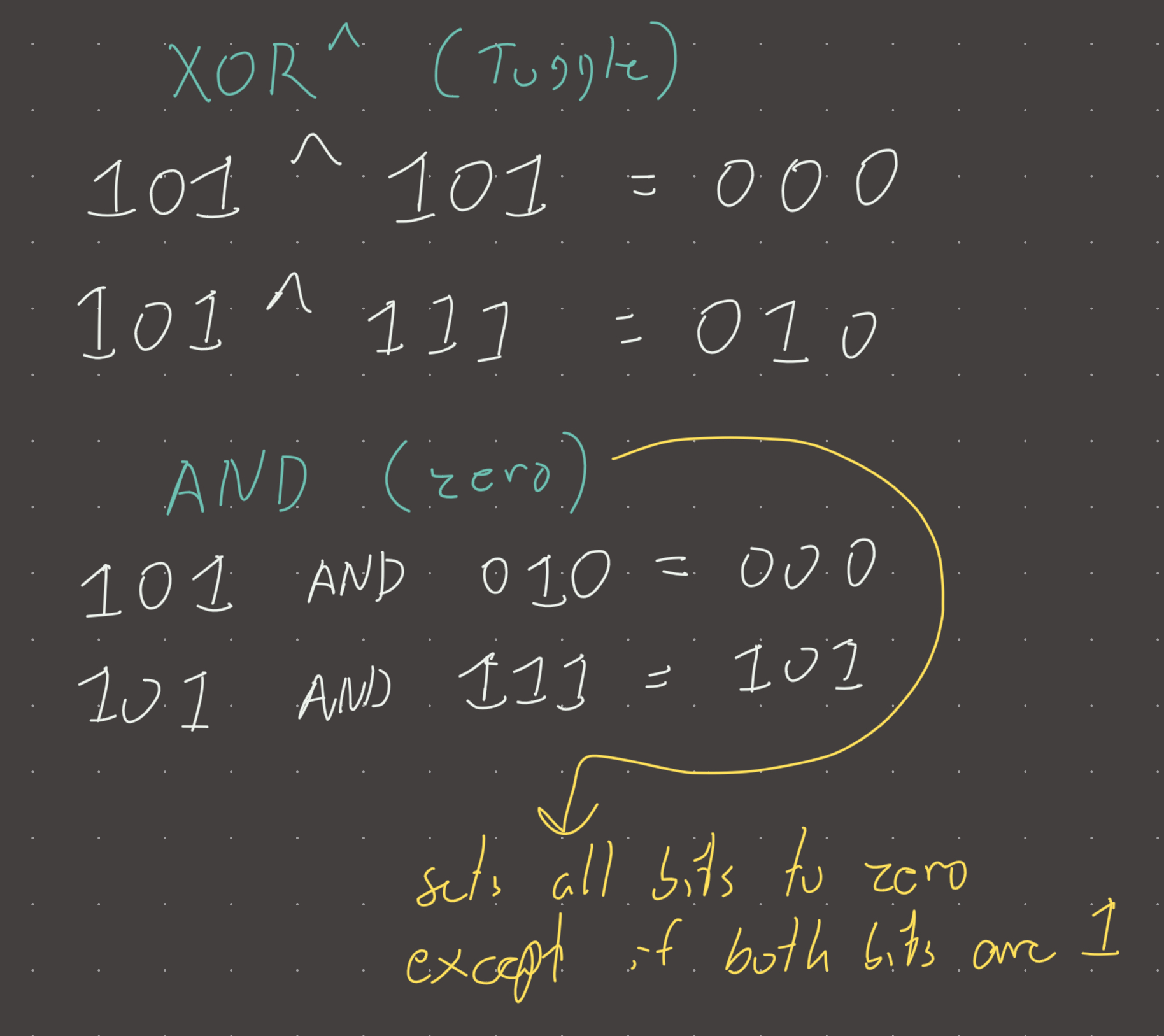
Review 1
Solved it almost instantly with a DFS and binary array. Bitwise is slightly better but whatever.