Word break

Link: https://leetcode.com/problems/word-break/

Solution:

Topics: BFS, DP, Word break II

Intuition
My first solution was actually DP similar to Word break II, but the most efficient solution is actually BFS. I think its worth going through the BFS solution because its very elegant, yet very subtle mainly because DP is the more obvious path.

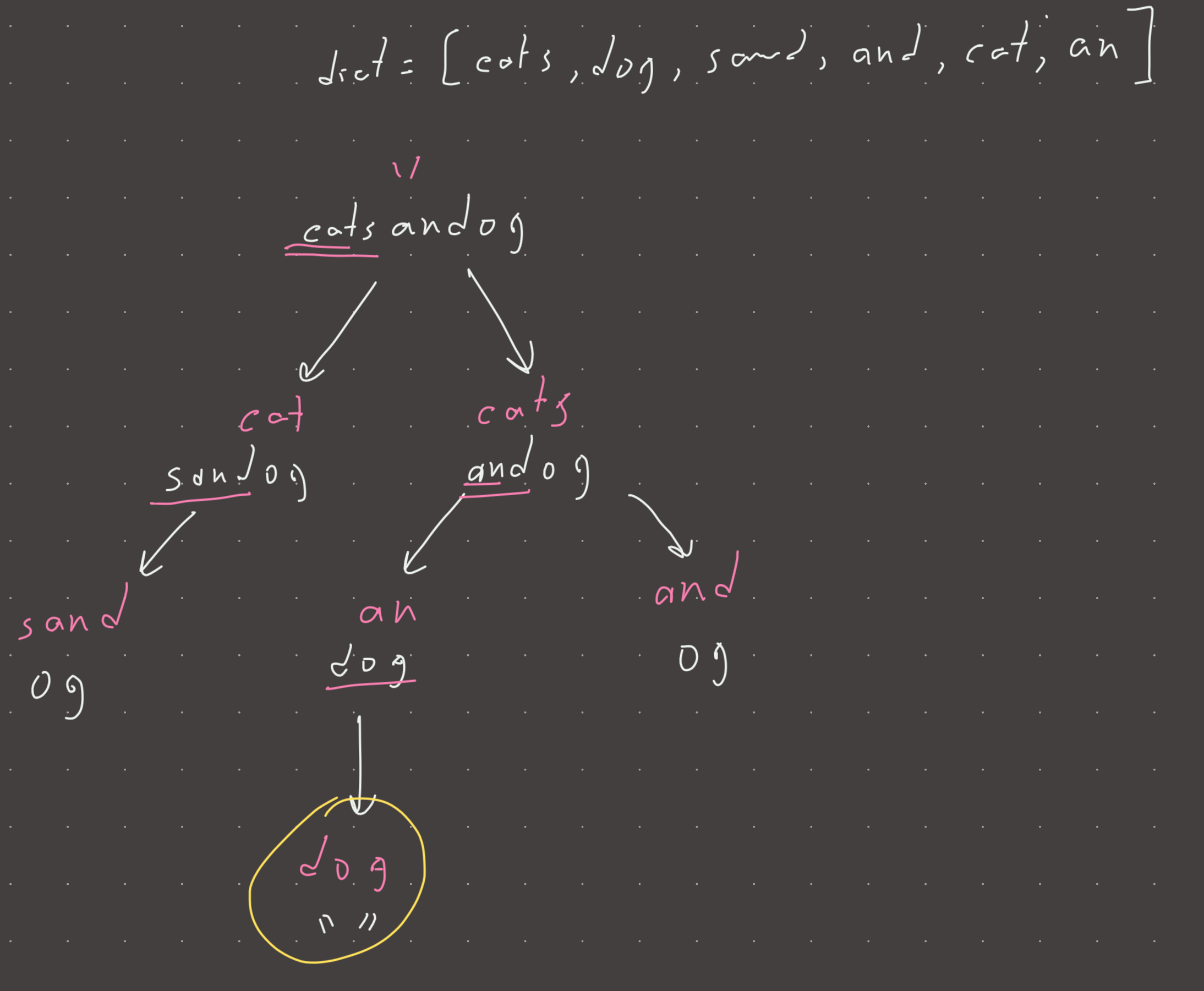
The key intuition for the BFS solution is realizing that (unlike Word break II), all we are asked is can the word be broken up or not. There are potentially many ways to break up the string, and the recursive DP solution (like in Word break II) would be forced to explore all of them. But the problem only asks for one, so if we frame this as a shortest path problem (break the string into the least amount of words), then we can skip exploring ALL the ways the string can be broken and just early exit our BFS (return True), when a way to break has been found.

Implementation (BFS)

def word_break(wordDict, s):
	word_dict = set(wordDict)
	seen = set()
	queue = deque([0])
	while queue:
		start = queue.popleft()
		if start == len(s):
			return True
		if start in seen:
			continue
		seen.add(start)
		for end in range(start+1, len(s)+1):
			if s[start:end] in word_dict:
				queue.append(end)
	return False
	
#time: o(n**3) because there are len(s) nodes and we slice s an each index (n^2)
#memory: o(n)

This is the optimized DP solution with only one cached variable (as opposed to 2 in Word break II). The time and memory complexity is the same as the BFS solution, but BFS is still a bit better because I think in the DP case there is no guarantee that the “way” found will be the shortest one.

Implementation (DP)

def word_break(wordDict, s):
	word_dict = set(wordDict)
	@cache
	def dfs(start):
		if start == len(s):
			return True
		for end in range(start+1, len(s)+1):
			if s[start:end] in word_dict:
				if dfs(end):
					return True
		return False
 
	return dfs(0)
	
#time: o(n**3)
#memory: o(n)

Visual

Review 1
There are some small errors in my editorial. The BFS solution is not more efficient than the cached DP one. They are the same. The reason we can cache this DFS function and not the one in Word break II is because in that one we actually want all the ways the end can be reached. In this one we don’t care about all the possibilities…so caching the function is effectively terminating the recursion early as soon as a positive result is reached! The depth of this tree is the time complexity and it should also be the shortest path.

So I think the DP solution is the correct approach here after all. This is a pretty niche application of BFS and does not generically apply to most problems of this type. The only subtle part of the DP solution is the realizing that we need to cache because the actual path doesn’t matter, we only need one.

review
hard